题目大意:Misha和Andrew在玩游戏。规则是:在1~n的整数中,Misha选一个数m,Andrew选一个数a,再随机选一个数c,选择的数更接近c的人获胜,若一样,则Misha获胜。现在已知n和m,要选一个数作为a,使Andrew获胜的可能性最大。
若$a=m$,则总是Misha胜,不考虑,所以$a$要么大于$m$,要么小于$m$。
以$a<m$为例。若$c\ge m$,则总是Misha胜;若$c<m$,则在$a=m-1$时,总是Andrew获胜,否则Misha有获胜的可能。所以,$a=m-1$时Andrew获胜的可能性最大,为$\frac{m-1}{n}$
同理,若$a>m$,$a=m+1$时Andrew获胜的可能性最大,为$\frac{n-m}{n}$。
简单判断一下那种可能性大就用哪种,注意特判$n=1$的情况即可。
代码在此。
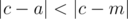 is maximal, where
is maximal, where  评论 (0)
评论 (0)