Peppa the Pig was walking and walked into the forest. What a strange coincidence! The forest has the shape of a rectangle, consisting of n rows and m columns. We enumerate the rows of the rectangle from top to bottom with numbers from 1 to n, and the columns — from left to right with numbers from 1 to m. Let's denote the cell at the intersection of the r-th row and the c-th column as (r, c).
Initially the pig stands in cell (1, 1), and in the end she wants to be in cell (n, m). Since the pig is in a hurry to get home, she can go from cell (r, c), only to either cell (r + 1, c) or (r, c + 1). She cannot leave the forest.
The forest, where the pig is, is very unusual. Some cells of the forest similar to each other, and some look very different. Peppa enjoys taking pictures and at every step she takes a picture of the cell where she is now. The path through the forest is considered to bebeautiful if photographs taken on her way, can be viewed in both forward and in reverse order, showing the same sequence of photos. More formally, the line formed by the cells in order of visiting should be a palindrome (you can read a formal definition of a palindrome in the previous problem).
Count the number of beautiful paths from cell (1, 1) to cell (n, m). Since this number can be very large, determine the remainder after dividing it by 109 + 7.
The first line contains two integers n, m (1 ≤ n, m ≤ 500) — the height and width of the field.
Each of the following n lines contains m lowercase English letters identifying the types of cells of the forest. Identical cells are represented by identical letters, different cells are represented by different letters.
Print a single integer — the number of beautiful paths modulo 109 + 7.
3 4 aaab baaa abba
3
Picture illustrating possibilities for the sample test.
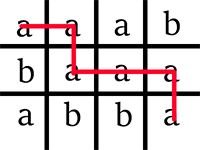
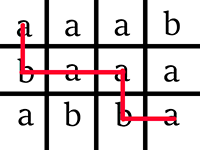
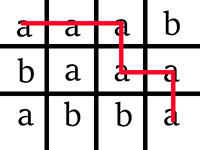
题目大意:给出一个n×m的矩形,每一格有一个字母,问从左上角走到右下角(每次只能向下走或向右走一格)使经过的字母序列为回文串的方案数对$10^9+7$取模后的值。
问题转化为两个人同时从左上角和右下角开始走,每次走时两者走到的位置的字母一样,最终走到同一格或相邻格的方案数。设$f(i,x_1,x_2)$表示已经走了i步,第一个人走到第$x_1$行,第二个人走到第$x_2$行的方案数。两人分别走到哪一列可以通过这3个数算出来。
递推式:
$f(i,x1,x2)=f(i-1,x1,x2)+f(i-1,x1-1,x2)\\ +f(i-1,x1,x2+1)+f(i-1,x1-1,x2+1)$
注意总步数的奇偶性以及取模。
代码在此。
 评论 (0)
评论 (0)