You are given two arrays A and B consisting of integers, sorted in non-decreasing order. Check whether it is possible to choose knumbers in array A and choose m numbers in array B so that any number chosen in the first array is strictly less than any number chosen in the second array.
The first line contains two integers nA, nB (1 ≤ nA, nB ≤ 105), separated by a space — the sizes of arrays A and B, correspondingly.
The second line contains two integers k and m (1 ≤ k ≤ nA, 1 ≤ m ≤ nB), separated by a space.
The third line contains nA numbers a1, a2, ... anA ( - 109 ≤ a1 ≤ a2 ≤ ... ≤ anA ≤ 109), separated by spaces — elements of array A.
The fourth line contains nB integers b1, b2, ... bnB ( - 109 ≤ b1 ≤ b2 ≤ ... ≤ bnB ≤ 109), separated by spaces — elements of array B.
Print "YES" (without the quotes), if you can choose k numbers in array A and m numbers in array B so that any number chosen in arrayA was strictly less than any number chosen in array B. Otherwise, print "NO" (without the quotes).
3 3 2 1 1 2 3 3 4 5
YES
3 3 3 3 1 2 3 3 4 5
NO
5 2 3 1 1 1 1 1 1 2 2
YES
In the first sample test you can, for example, choose numbers 1 and 2 from array A and number 3 from array B (1 < 3 and 2 < 3).
In the second sample test the only way to choose k elements in the first array and m elements in the second one is to choose all numbers in both arrays, but then not all the numbers chosen in A will be less than all the numbers chosen in B: 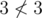 .
.
题目大意:给出两个非降序的序列A和B<,长度分别为$n_A$和$n_B$,问是否有可能在A中选k个数,B中选m个数,使在A中选的数都严格小于B中选的数。
A中选前k个数,B中选后m个数,若$A_k<B_{n_B-m+1}$,则满足题目的条件。
代码在此。
 评论 (0)
评论 (0)