You've got array A, consisting of n integers and a positive integer k. Array A is indexed by integers from 1 to n.
You need to permute the array elements so that value
The first line contains two integers n, k (2 ≤ n ≤ 3·105, 1 ≤ k ≤ min(5000, n - 1)).
The second line contains n integers A[1], A[2], ..., A[n] ( - 109 ≤ A[i] ≤ 109), separate by spaces — elements of the array A.
Print the minimum possible value of the sum described in the statement.
3 2 1 2 4
1
5 2 3 -5 3 -5 3
0
6 3 4 3 4 3 2 5
3
In the first test one of the optimal permutations is 1 4 2.
In the second test the initial order is optimal.
In the third test one of the optimal permutations is 2 3 4 4 3 5.
题目大意：给出一个序列a和一个正整数k，重新排列序列使$\sum_{i=1}^{n-k}\left|a_i-a_{i+k}\right|$最小，输出它的最小值。
这题比较神，我就翻译官方题解了。。。
我们可以用它们模k的结果把序号1~n分组。当计算题目中的那个式子时，我们可以分别考虑每个组并且把各组中相邻数字的差距加起来。
考虑其中一组，它包括序号模k的结果为i的数字，即$\left\{ a_j|j\equiv i\pmod{k}\right\}$。让我们从左到右把它们写下来：$b_1,b_2,...,b_m$。那么这组对结果的贡献为$\sum_{j=1}^{m-1}\left|b_j-b_{j+1}\right|$。我们可以注意到如果我们对$b_1,...,b_m$按非降序排列，结果不会增加。所以，在优化后的结果中，我们可以把各组数字看成是非降序的。更进一步，在这种情况下这组的贡献等于$\left|b_m-b_1\right|$。
现在考虑两组$b_1,...,b_m$和$c_1,c_2,...,c_l$，它们都按非降序排列。我们可以确定要么$b_1\ge c_l$要么$b_m\le c_1$，也就是说，线段$\left[b_1,b_m\right]$和$\left[c_1,c_l\right]$只能在它们的端点上用公共点。
为什么是这样？这两组对结果的贡献为$\left[b_m-b_1\right]+\left[c_l-c_1\right]$。我们考虑$c_1\ge b_1$的情况，另一种情况是类似的。如果$c_1<b_m$，那么交换$c_1$和$b_m$不会增加这两组对结果的贡献，因为b组的右边界向左移了，而c组的左边界向右移了。所以，在$c_1\ge b_m$的情况下，前面的断言被证明了。
现在我们知道各组的数字应该是来自排序后的原序列构成的连续线段。事实上，我们有$k-\left(n\bmod k\right)$个大小为$\frac{n}{k}$的组（所以叫它小组），和$n\bmod k$个大小为$\frac{n}{k}+1$的组（所以叫它大组）。考虑下面的DP：$dp\left(L,S\right)$——如果我们从排好序的原序列的元素中选取开始的$L\times\left(\frac{n}{k}+1\right)+S\times\frac{n}{k}$L个大组和S个小组对结果的最小贡献。状态数不会超过$O\left(k^2\right)$，每个转移可以优化到$O\left(1\right)$：我们选择加入大组或小组并且通过对序列中的两个元素做减法获得加入结果中的值，最终答案是$dp\left(n\bmod k,k-\left(n\bmod k\right)\right)$
解决方案的最终时间复杂度为$O\left(n\log_2 n+k^2\right)$。我们可以注意到在pretests中$n\bmod k$非常小，所以一些较慢的解决方案可以通过，但是它们在final tests中不能通过。
我英语太弱了，有些地方翻译得比较差，望谅解。
代码在此。
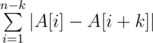
评论 (0)
