题目大意:
一个由若干个数对$\left(a,b\right)\left(a,b\in A\right)$组成的集合$\rho$被称为一个集合A上的二元关系。若$\left(a,b\right)\in\rho$,则a,b满足二元关系$\rho$,记作$a\mathop{\sim}^\rho b$。
如果满足一下三个性质,一个二元关系是相等关系。
1. 自反性:$\forall a,\,a\mathop{\sim}^\rho a$
2. 对称性:$\forall a\mathop{\sim}^\rho b,\,b\mathop{\sim}^\rho a$
3. 传递性:$\forall a\mathop{\sim}^\rho b,b\mathop{\sim}^\rho c,\,a\mathop{\sim}^\rho c$
Little Johnny发现第一条是没有必要的,因为$a\mathop{\sim}^\rho b\Rightarrow b\mathop{\sim}^\rho a\Rightarrow a\mathop{\sim}^\rho a$。
显然他的证明是错误的,所以求一个有n个元素的集合上的满足对称性和传递性但不满足自反性的二元关系的个数。
只要$\exists a\in A,\nexists a\mathop{\sim}^\rho b\left(b\in A\right)$就行了,所以答案是$\sum_{i=0}^{n-1}C_n^i\times B_i$。
$C_n^i$表示在n个元素中任选i个元素的方法数,这i个元素和其他元素有关系,剩余的元素则没有。
$B_i$是贝尔数,把i个元素分成若干个非空集合的方法数。表示把有关系的i个元素分成若干个非空集合,在同一个集合中的元素满足关系。
代码在此。
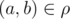 , in this case we use a notation
, in this case we use a notation  .
. );
);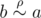 );
);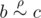 , than
, than  ).
).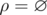 . In other words, for a single element
. In other words, for a single element 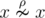 .
. 评论 (0)
评论 (0)