题目大意:给出平面上的n个点$\left(x_i,y_i\right)$,定义$dist\left(i,j\right)=\left|x_i-x_j\right|+\left|y_i-y_j\right|$,求1~n的一个排列p,使得$\sum_{i=1}^{n-1}dist\left(p_i,p_{i+1}\right)\leq 2.5\times 10^9$。
将所有点按纵坐标分组,纵坐标1~1000一组,1001~2000一组,依此类推,每组都按横坐标排序,然后按之字形走,易证结果一定不会超过要求的值。
代码是用C#的LINQ写的,看不懂就算了。。
代码在此。
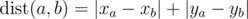 (the distance calculated by such formula is called
(the distance calculated by such formula is called 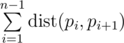 .
.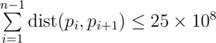 .
.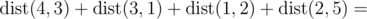
 评论 (0)
评论 (0)