There is a polyline going through points (0, 0) – (x, x) – (2x, 0) – (3x, x) – (4x, 0) – ... - (2kx, 0) – (2kx + x, x) – ....
We know that the polyline passes through the point (a, b). Find minimum positive value x such that it is true or determine that there is no such x.
Only one line containing two positive integers a and b (1 ≤ a, b ≤ 109).
Output the only line containing the answer. Your answer will be considered correct if its relative or absolute error doesn't exceed 10 - 9. If there is no such x then output - 1 as the answer.
3 1
1.000000000000
1 3
-1
4 1
1.250000000000
You can see following graphs for sample 1 and sample 3.
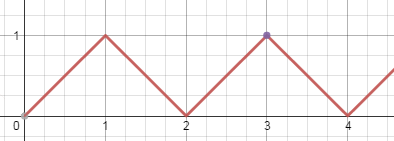
题目大意：有一条折线经过这些点：
$\left(0,0\right)-\left(x,x\right)-\left(2x,0\right)-\left(3x,x\right)-\left(4x,0\right)-...$
现已知一个点$\left(a,b\right)$经过这个点，求最小的x。
易知折线必定经过点$\left(a-b,0\right)$或点$\left(a+b,0\right)$（$b>a$则无解），这里以后者为例。
x一定不小于b，所以从$\left(0,0\right)$到$\left(a+b,0\right)$的折线与x轴形成的三角形个数为$\lfloor\frac{\left(a+b\right)}{2b}\rfloor$，那么最小的x就是$\frac{a+b}{2\lfloor\frac{a+b}{2b}\rfloor}$。
a-b的情况也可以类似地计算，实际上，a+b的情况一定比a-b的情况更优。
代码在此。
评论 (0)
