[Codeforces Round #327 (Div. 2)] 我的第一场Cf现场赛

11
5
2015

做这场比赛是上上个星期的事了，今天终于想起来把题解写掉。

Harry Potter and He-Who-Must-Not-Be-Named engaged in a fight to the death once again. This time they are located at opposite ends of the corridor of length l. Two opponents simultaneously charge a deadly spell in the enemy. We know that the impulse of Harry's magic spell flies at a speed of p meters per second, and the impulse of You-Know-Who's magic spell flies at a speed of q meters per second.

The impulses are moving through the corridor toward each other, and at the time of the collision they turn round and fly back to those who cast them without changing their original speeds. Then, as soon as the impulse gets back to it's caster, the wizard reflects it and sends again towards the enemy, without changing the original speed of the impulse.

Since Harry has perfectly mastered the basics of magic, he knows that after the second collision both impulses will disappear, and a powerful explosion will occur exactly in the place of their collision. However, the young wizard isn't good at math, so he asks you to calculate the distance from his position to the place of the second meeting of the spell impulses, provided that the opponents do not change positions during the whole fight.

Input

The first line of the input contains a single integer l (1 ≤ l ≤ 1 000) — the length of the corridor where the fight takes place.

The second line contains integer p, the third line contains integer q (1 ≤ p, q ≤ 500) — the speeds of magical impulses for Harry Potter and He-Who-Must-Not-Be-Named, respectively.

Output

Print a single real number — the distance from the end of the corridor, where Harry is located, to the place of the second meeting of the spell impulses. Your answer will be considered correct if its absolute or relative error will not exceed 10 - 4.

Namely: let's assume that your answer equals a, and the answer of the jury is b. The checker program will consider your answer correct if 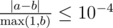$\text{[math]}$ .

							Sample test(s)

									input
100
50
50

									output
50

									input
199
60
40

									output
119.4

Note

In the first sample the speeds of the impulses are equal, so both of their meetings occur exactly in the middle of the corridor.

题目大意：在一条长为l的走廊里，哈利波特和“那个人”在两端分别向对方放一个魔法，两个魔法的前进速度分别是p和q。两个魔法在第一次相遇时会以原速度往回走，在碰到走廊两端时又会以原速度被反弹，它们在第二次相遇时会爆炸，求爆炸位置与哈利波特的距离。

分情况讨论乱搞。我做的时候被实数萎了半天，半个小时才做完。。

The name of one small but proud corporation consists of n lowercase English letters. The Corporation has decided to try rebranding — an active marketing strategy, that includes a set of measures to change either the brand (both for the company and the goods it produces) or its components: the name, the logo, the slogan. They decided to start with the name.

For this purpose the corporation has consecutively hired m designers. Once a company hires the i-th designer, he immediately contributes to the creation of a new corporation name as follows: he takes the newest version of the name and replaces all the letters xiby yi, and all the letters yi by xi. This results in the new version. It is possible that some of these letters do no occur in the string. It may also happen that xi coincides with yi. The version of the name received after the work of the last designer becomes the new name of the corporation.

Manager Arkady has recently got a job in this company, but is already soaked in the spirit of teamwork and is very worried about the success of the rebranding. Naturally, he can't wait to find out what is the new name the Corporation will receive.

Satisfy Arkady's curiosity and tell him the final version of the name.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 200 000) — the length of the initial name and the number of designers hired, respectively.

The second line consists of n lowercase English letters and represents the original name of the corporation.

Next m lines contain the descriptions of the designers' actions: the i-th of them contains two space-separated lowercase English lettersxi and yi.

Output

Print the new name of the corporation.

							Sample test(s)

									input
6 1
police
p m

									output
molice

									input
11 6
abacabadaba
a b
b c
a d
e g
f a
b b

									output
cdcbcdcfcdc

Note

In the second sample the name of the corporation consecutively changes as follows:

$\text{[math]}$

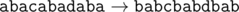
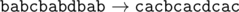
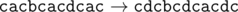
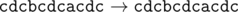
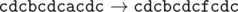
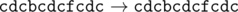
题目大意：给出一个长度为n的字符串。有m个操作，第i个操作$\left(x_i,y_i\right)$表示把字符串中所有字母$x_i$替换为$y_i$，求操作结束后的字符串。字符串中只有小写字母。

用一个数组记下原字符串的某个字母最终会被替换成什么字母，每次操作时更新这个数组，最后根据这个数组就可以用原串求出结果。

A schoolboy named Vasya loves reading books on programming and mathematics. He has recently read an encyclopedia article that described the method of median smoothing (or median filter) and its many applications in science and engineering. Vasya liked the idea of the method very much, and he decided to try it in practice.

Applying the simplest variant of median smoothing to the sequence of numbers a1, a2, ..., an will result a new sequence b1, b2, ..., bnobtained by the following algorithm:

b1 = a1, bn = an, that is, the first and the last number of the new sequence match the corresponding numbers of the original sequence.
For i = 2, ..., n - 1 value bi is equal to the median of three values ai - 1, ai and ai + 1.

The median of a set of three numbers is the number that goes on the second place, when these three numbers are written in the non-decreasing order. For example, the median of the set 5, 1, 2 is number 2, and the median of set 1, 0, 1 is equal to 1.

In order to make the task easier, Vasya decided to apply the method to sequences consisting of zeros and ones only.

Having made the procedure once, Vasya looked at the resulting sequence and thought: what if I apply the algorithm to it once again, and then apply it to the next result, and so on? Vasya tried a couple of examples and found out that after some number of median smoothing algorithm applications the sequence can stop changing. We say that the sequence is stable, if it does not change when the median smoothing is applied to it.

Now Vasya wonders, whether the sequence always eventually becomes stable. He asks you to write a program that, given a sequence of zeros and ones, will determine whether it ever becomes stable. Moreover, if it ever becomes stable, then you should determine what will it look like and how many times one needs to apply the median smoothing algorithm to initial sequence in order to obtain a stable one.

Input

The first input line of the input contains a single integer n (3 ≤ n ≤ 500 000) — the length of the initial sequence.

The next line contains n integers a1, a2, ..., an (ai = 0 or ai = 1), giving the initial sequence itself.

Output

If the sequence will never become stable, print a single number - 1.

Otherwise, first print a single integer — the minimum number of times one needs to apply the median smoothing algorithm to the initial sequence before it becomes is stable. In the second line print n numbers separated by a space — the resulting sequence itself.

							Sample test(s)

									input
4
0 0 1 1

									output
0
0 0 1 1

									input
5
0 1 0 1 0

									output
2
0 0 0 0 0

Note

In the second sample the stabilization occurs in two steps: 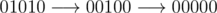$\text{[math]}$ , and the sequence 00000 is obviously stable.

题目大意：给出一个01序列，定义一个操作为使序列的两端不变，其余各个元素变为它自己和它左右两个元素的中位数，求至少多少次操作后再执行操作操作不会使序列发生改变，并输出这个最终序列。

通过观察可以发现操作只会修改序列中01交替出现的部分，分别考虑这些部分，就可以$O\left(n\right)$求出答案。

A team of furry rescue rangers was sitting idle in their hollow tree when suddenly they received a signal of distress. In a few moments they were ready, and the dirigible of the rescue chipmunks hit the road.

We assume that the action takes place on a Cartesian plane. The headquarters of the rescuers is located at point (x1, y1), and the distress signal came from the point (x2, y2).

Due to Gadget's engineering talent, the rescuers' dirigible can instantly change its current velocity and direction of movement at any moment and as many times as needed. The only limitation is: the speed of the aircraft relative to the air can not exceed $\text{[math]}$ meters per second.

Of course, Gadget is a true rescuer and wants to reach the destination as soon as possible. The matter is complicated by the fact that the wind is blowing in the air and it affects the movement of the dirigible. According to the weather forecast, the wind will be defined by the vector (vx, vy) for the nearest t seconds, and then will change to (wx, wy). These vectors give both the direction and velocity of the wind. Formally, if a dirigible is located at the point (x, y), while its own velocity relative to the air is equal to zero and the wind (ux, uy) is blowing, then after $\text{[math]}$ seconds the new position of the dirigible will be $\text{[math]}$ .

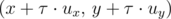Gadget is busy piloting the aircraft, so she asked Chip to calculate how long will it take them to reach the destination if they fly optimally. He coped with the task easily, but Dale is convinced that Chip has given the random value, aiming only not to lose the face in front of Gadget. Dale has asked you to find the right answer.

It is guaranteed that the speed of the wind at any moment of time is strictly less than the maximum possible speed of the airship relative to the air.

Input

The first line of the input contains four integers x1, y1, x2, y2 (|x1|, |y1|, |x2|, |y2| ≤ 10 000) — the coordinates of the rescuers' headquarters and the point, where signal of the distress came from, respectively.

The second line contains two integers $\text{[math]}$ and t (0 < v, t ≤ 1000), which are denoting the maximum speed of the chipmunk dirigible relative to the air and the moment of time when the wind changes according to the weather forecast, respectively.

Next follow one per line two pairs of integer (vx, vy) and (wx, wy), describing the wind for the first t seconds and the wind that will blow at all the remaining time, respectively. It is guaranteed that 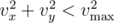$\text{[math]}$ and $\text{[math]}$ .

Output

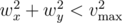Print a single real value — the minimum time the rescuers need to get to point (x2, y2). You answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if 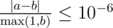$\text{[math]}$ .

							Sample test(s)

									input
0 0 5 5
3 2
-1 -1
-1 0

									output
3.729935587093555327

									input
0 0 0 1000
100 1000
-50 0
50 0

									output
11.547005383792516398

题目大意：在一个二维坐标系中，给出起点，终点，最大前进速度，前t秒的风速，t秒后的风速。速度均以向量的形式给出，保证风速严格小于最大前进速度。求最快多久能从起点到达终点。

因为风速小于前进速度，易证如果x秒内能到达终点，则用超过x秒的时间也一定能到达终点，也就是说答案是单调的，直接二分答案即可求出解。

The famous global economic crisis is approaching rapidly, so the states of Berman, Berance and Bertaly formed an alliance and allowed the residents of all member states to freely pass through the territory of any of them. In addition, it was decided that a road between the states should be built to guarantee so that one could any point of any country can be reached from any point of any other State.

Since roads are always expensive, the governments of the states of the newly formed alliance asked you to help them assess the costs. To do this, you have been issued a map that can be represented as a rectangle table consisting of n rows and m columns. Any cell of the map either belongs to one of three states, or is an area where it is allowed to build a road, or is an area where the construction of the road is not allowed. A cell is called passable, if it belongs to one of the states, or the road was built in this cell. From any passable cells you can move up, down, right and left, if the cell that corresponds to the movement exists and is passable.

Your task is to construct a road inside a minimum number of cells, so that it would be possible to get from any cell of any state to any cell of any other state using only passable cells.

It is guaranteed that initially it is possible to reach any cell of any state from any cell of this state, moving only along its cells. It is also guaranteed that for any state there is at least one cell that belongs to it.

Input

The first line of the input contains the dimensions of the map n and m (1 ≤ n, m ≤ 1000) — the number of rows and columns respectively.

Each of the next n lines contain m characters, describing the rows of the map. Digits from 1 to 3 represent the accessory to the corresponding state. The character '.' corresponds to the cell where it is allowed to build a road and the character '#' means no construction is allowed in this cell.

Output

Print a single integer — the minimum number of cells you need to build a road inside in order to connect all the cells of all states. If such a goal is unachievable, print -1.

							Sample test(s)

									input
4 5
11..2
#..22
#.323
.#333

									output
2

									input
1 5
1#2#3

									output
-1

题目大意：在一张n×m的地图上，有3个连通块。在不属于任何一个连通块的地方，有些可以修路，有些不能。从任意连通块的任意一点出发，可以前往其上下左右任意一个点，只要目标点修了路或者它是某个连通块的一部分。现在要在一些点修路，使得在3个连通块中的任意两点都互相可达。求最少的要修路的点数。

要使3个连通块互相联通，有两种可能：某两个连通块修路到第3个连通块，或分别从3个连通块出发修路并交汇在某一点。分别计算从3个连通块出发到其他点的最短距离。第一种情况可以直接计算，第二种情况也可以枚举交汇点来计算。注意求最短距离时如果用SPFA或Dijkstra很容易TLE，用BFS却跑得很快。

这场比赛所有代码在此。

Category: 题解 | Tags: 模拟二分图论 Codeforces 最短路 | Read Count: 660

Stalker's Blog

I am here in the shadows.