NOIP结束后，感觉要爆蛋了，天天都在浪，于是决定打场VP冷静一下。
题目大意：给出n和t（$t\in\left[2,10\right]$），求一个可以被t整除的n位数。
如果t为10且n为1则无解，否则答案的最高位是t（t为10的话最高位为1），后面跟着n-1个0。
Kolya loves putting gnomes at the circle table and giving them coins, and Tanya loves studying triplets of gnomes, sitting in the vertexes of an equilateral triangle.
More formally, there are 3n gnomes sitting in a circle. Each gnome can have from 1 to 3 coins. Let's number the places in the order they occur in the circle by numbers from 0 to 3n - 1, let the gnome sitting on the i-th place have ai coins. If there is an integer i (0 ≤ i < n) such that ai + ai + n + ai + 2n ≠ 6, then Tanya is satisfied.
Count the number of ways to choose ai so that Tanya is satisfied. As there can be many ways of distributing coins, print the remainder of this number modulo 109 + 7. Two ways, a and b, are considered distinct if there is index i (0 ≤ i < 3n), such that ai ≠ bi (that is, some gnome got different number of coins in these two ways).
A single line contains number n (1 ≤ n ≤ 105) — the number of the gnomes divided by three.
Print a single number — the remainder of the number of variants of distributing coins that satisfy Tanya modulo 109 + 7.
1
20
2
680
20 ways for n = 1 (gnome with index 0 sits on the top of the triangle, gnome 1 on the right vertex, gnome 2 on the left vertex):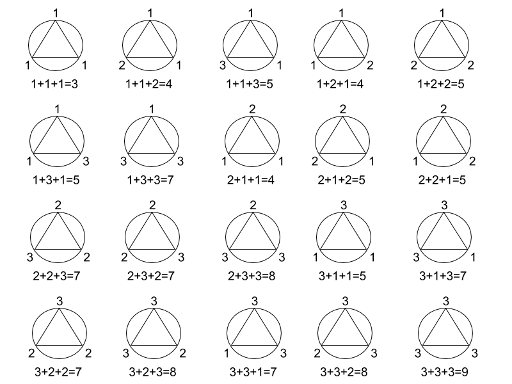
题目大意：在一个圆上有3n个点，依次编号，相邻两点间距离相等。每个点上可以放1~3个硬币，设$a_i$为第i个点的硬币数。求有多少种放硬币的方案满足至少存在一个i使$a_i+a_{i+n}+a_{i+2n}\neq 6$。
正解是$3^{3n}-7^n$。但是我太弱了，没有想到，于是用了个很麻烦的做法。枚举有多少个i满足$a_i+a_{i+n}+a_{i+2n}=6$，分别计算答案，最终答案是$\sum_{i=0}^{n-1}7^i\times 20^{n-i}C_n^i$。
题目大意：定义$f\left(a,b\right)$为长度相等的字符串a，b的对应位置字符不同的个数。给出字符串s1，s2，求一个字符串s3，使$f\left(s1,s3\right)=f\left(s2,s3\right)=t$（t已给出）。
类似f的定义，可以定义$g\left(a,b\right)$为对应位置字符相同的个数，题目可以转化为求s3使$g\left(s1,s3\right)=g\left(s2,s3\right)=n-t$。优先选择s1和s2对应对应相等的位置，设这样的位置有cnt个。如果$cnt\ge n-t$，选择n-t个这样的位置和s3相同，所有剩下位置都和s3不同。否则就还需要$\left(n-t-cnt\right)\times 2$个s1和s2不同的位置，使s3在这些位置上一半和s1相等，一半和s2相等。如果找不到足够的位置，则无解。
Dima loves representing an odd number as the sum of multiple primes, and Lisa loves it when there are at most three primes. Help them to represent the given number as the sum of at most than three primes.
More formally, you are given an odd numer n. Find a set of numbers pi (1 ≤ i ≤ k), such that
- 1 ≤ k ≤ 3
- pi is a prime
-
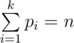
The numbers pi do not necessarily have to be distinct. It is guaranteed that at least one possible solution exists.
The single line contains an odd number n (3 ≤ n < 109).
In the first line print k (1 ≤ k ≤ 3), showing how many numbers are in the representation you found.
In the second line print numbers pi in any order. If there are multiple possible solutions, you can print any of them.
27
3 5 11 11
A prime is an integer strictly larger than one that is divisible only by one and by itself.
题目大意：给出一个大于等于3的奇数n，要把它分解成1~3个质数的和。
如果n是质数，就直接输出它，如果n-2是质数，就输出2和n-2，否则就暴力枚举判断。居然能过。。。
题目大意：给出1~n的2个排列p和s，每次可以交换p中的两个元素$p_i,p_j$，代价为$\left|i-j\right|$。求把p变成s的最小代价及其方案。
考虑把p变成有序的排列的代价，这和题目要求是类似的。显然代价的最小值是$\frac{1}{2}\sum_{i=1}^n\left|i-p_i\right|$。可以证明这个最小值是可以取到的。
考虑要把n放到最右边，设$p_{pos}=n$，如果存在一个pos2使$pos<pos2$且$p_{pos2}\leq pos$，那么交换它们一定是优的。根据抽屉原理，在n移到最右边以前，这样的pos2总是存在。
所以只要不断重复这个算法，把当前的还没有放好的最大元素放过去就行了。
代码在此。
评论 (0)
