The GCD table G of size n × n for an array of positive integers a of length n is defined by formula
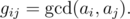
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both xand y, it is denoted as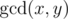 
. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:
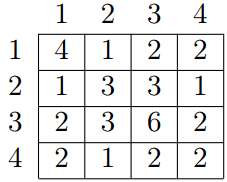
Given all the numbers of the GCD table G, restore array a.
The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n2 space-separated numbers — the elements of the GCD table of G for array a.
All the numbers in the table are positive integers, not exceeding 109. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.
In the single line print n positive integers — the elements of array a. If there are multiple possible solutions, you are allowed to print any of them.
4 2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2
4 3 6 2
1 42
42
2 1 1 1 1
1 1
题目大意：有一个长度为n的序列a，以乱序给出$gcd\left(a_i,a_j\right)\left(1\leq i,j\leq n\right)$，求原序列a。数据保证有解。
这题要利用gcd的一个性质：$gcd\left(i,j\right)\geq\max\left(i,j\right)$，所以给出的所有gcd中的最大值一定等于原序列中的最大值。然后就可以做了，每次取出最大的gcd值，它一定是a序列中还没有确定的元素中最大的那个，然后去掉它自己以及它和已经确定的其他元素的gcd，不断重复这一过程就可以还原出原序列。
代码在此。
评论 (0)
