题目大意:给出一个从0开始编号的无限循环序列a,它满足$a_i=a_{i\bmod n}\left(i\geq n\right)$,定义它的循环子段b$\left(l,s\right)\left(0\leq l<n,1\leq s<n\right)$为满足$b_i=a_{\left(i-l\right)\bmod s+l}$的循环序列。求a有多少个循环子段满足$b_i\geq a_i\left(i\geq l\right)$。
对于一个确定的s,有$a_i\geq a_j\left(i\equiv j\pmod{\gcd\left(n,s\right)}\right)$。于是可以枚举$g=\gcd\left(n,s\right)$,分别进行计算。考虑把$a_0...a_{n-1}$按照对g取模的值分成$\frac{n}{g}$组,显然b序列中的所有元素都必须是其对应的组中最大的那个。所以只需两个指针扫一下,把符合$\gcd\left(n,s\right)=g$的序列加入答案。注意扫的时候要注意一下循环序列式循环的。
因为g一定是n的因数,而n的因数个数大约有$\sqrt n$个,所以复杂度为$\mathcal{O}\left(n\sqrt n\right)$。
代码在此。
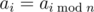 . A periodic subarray
. A periodic subarray
 评论 (0)
评论 (0)