While Duff was resting in the beach, she accidentally found a strange array b0, b1, ..., bl - 1 consisting of l positive integers. This array was strange because it was extremely long, but there was another (maybe shorter) array, a0, ..., an - 1 that b can be build from a with formula: bi = ai mod n where a mod b denoted the remainder of dividing a by b.
Duff is so curious, she wants to know the number of subsequences of b like bi1, bi2, ..., bix (0 ≤ i1 < i2 < ... < ix < l), such that:
- 1 ≤ x ≤ k
-
For each 1 ≤ j ≤ x - 1,
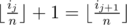
- For each 1 ≤ j ≤ x - 1, bij ≤ bij + 1. i.e this subsequence is non-decreasing.
Since this number can be very large, she want to know it modulo 109 + 7.
Duff is not a programmer, and Malek is unavailable at the moment. So she asked for your help. Please tell her this number.
The first line of input contains three integers, n, l and k (1 ≤ n, k, n × k ≤ 106 and 1 ≤ l ≤ 1018).
The second line contains n space separated integers, a0, a1, ..., an - 1 (1 ≤ ai ≤ 109 for each 0 ≤ i ≤ n - 1).
Print the answer modulo 1 000 000 007 in one line.
3 5 3 5 9 1
10
5 10 3 1 2 3 4 5
25
In the first sample case,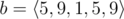 
. So all such sequences are: 
, 
, 
, 
, 
, 
, 
, 
, 
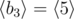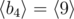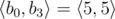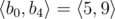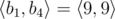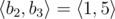and 
.
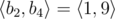题目大意：给出一个长度为n的序列b，有一个长度为l的序列a满足$a_i=b_{i\bmod n}$。求有多少个序列c，设它的长度为x，则它满足：$1\leq x\leq k$，$\lfloor\frac{c_i}{n}\rfloor+1=\lfloor\frac{c_{i+1}}{n}\rfloor$，$b_{c_i}\leq b_{c_{i+1}}$。
设$f\left(i,j\right)$表示长度为i，最后一个元素为j的c序列的个数，把$a_i$离散一下以后DP。
代码在此。
评论 (0)
