The semester is already ending, so Danil made an effort and decided to visit a lesson on harmony analysis to know how does the professor look like, at least. Danil was very bored on this lesson until the teacher gave the group a simple task: find 4 vectors in 4-dimensional space, such that every coordinate of every vector is 1 or - 1 and any two vectors are orthogonal. Just as a reminder, two vectors in n-dimensional space are considered to be orthogonal if and only if their scalar product is equal to zero, that is:
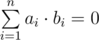
Danil quickly managed to come up with the solution for this problem and the teacher noticed that the problem can be solved in a more general case for 2k vectors in 2k-dimensinoal space. When Danil came home, he quickly came up with the solution for this problem. Can you cope with it?
The only line of the input contains a single integer k (0 ≤ k ≤ 9).
Print 2k lines consisting of 2k characters each. The j-th character of the i-th line must be equal to ' * ' if the j-th coordinate of the i-th vector is equal to - 1, and must be equal to ' + ' if it's equal to + 1. It's guaranteed that the answer always exists.
If there are many correct answers, print any.
2
++** +*+* ++++ +**+
Consider all scalar products in example:
- Vectors 1 and 2: ( + 1)·( + 1) + ( + 1)·( - 1) + ( - 1)·( + 1) + ( - 1)·( - 1) = 0
- Vectors 1 and 3: ( + 1)·( + 1) + ( + 1)·( + 1) + ( - 1)·( + 1) + ( - 1)·( + 1) = 0
- Vectors 1 and 4: ( + 1)·( + 1) + ( + 1)·( - 1) + ( - 1)·( - 1) + ( - 1)·( + 1) = 0
- Vectors 2 and 3: ( + 1)·( + 1) + ( - 1)·( + 1) + ( + 1)·( + 1) + ( - 1)·( + 1) = 0
- Vectors 2 and 4: ( + 1)·( + 1) + ( - 1)·( - 1) + ( + 1)·( - 1) + ( - 1)·( + 1) = 0
- Vectors 3 and 4: ( + 1)·( + 1) + ( + 1)·( - 1) + ( + 1)·( - 1) + ( + 1)·( + 1) = 0
题目大意:给出正整数$k$,求一个$2^k\times 2^k$的矩阵$A$,使得$a_{i,j}\in\left\{1,-1\right\},\forall i,j\in\left[1,2^k\right]\left(i\neq j\right)\ \sum_\limits{x=1}^\limits{2^k}a_{i,x}\cdot a_{j,x}=0$。
在打比赛时完全没有思路,于是这场我只做了前两题。。。
根据官方题解:递归求解。对于$k=0$,答案就是$1$或者$-1$;对于$k=i$,答案是把$k=i-1$的答案放在四个角上,并对放在右下方的那个矩阵的所有元素取相反数。
证明什么的我就不管了,因为我觉得这解法完全是shi出来的,没有什么意义。
代码在此。
 评论 (0)
评论 (0)