3
8
2016
1

[Codeforces Round #345] 爆蛋了。。。

好不容易有一场正常时间的Cf可以打，结果还爆蛋了。。。

开场做A，做了好久才做出，还WA了两发；B的思路是对的，但是因为实现问题WA了两发，还以为想错了，浪费了很久时间；C没开long long结果FST了；D没调出来；E当时不会做，今天发现是道傻逼题。

A. Joysticks
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

Friends are going to play console. They have two joysticks and only one charger for them. Initially first joystick is charged at a1 percent and second one is charged at a2 percent. You can connect charger to a joystick only at the beginning of each minute. In one minute joystick either discharges by 2 percent (if not connected to a charger) or charges by 1 percent (if connected to a charger).

Game continues while both joysticks have a positive charge. Hence, if at the beginning of minute some joystick is charged by 1 percent, it has to be connected to a charger, otherwise the game stops. If some joystick completely discharges (its charge turns to 0), the game also stops.

Determine the maximum number of minutes that game can last. It is prohibited to pause the game, i. e. at each moment both joysticks should be enabled. It is allowed for joystick to be charged by more than 100 percent.

Input

The first line of the input contains two positive integers a1 and a2 (1 ≤ a1, a2 ≤ 100), the initial charge level of first and second joystick respectively.

Output

Output the only integer, the maximum number of minutes that the game can last. Game continues until some joystick is discharged.

Examples
input
3 5
output
6
input
4 4
output
5
Note

In the first sample game lasts for 6 minute by using the following algorithm:

  • at the beginning of the first minute connect first joystick to the charger, by the end of this minute first joystick is at 4%, second is at 3%;
  • continue the game without changing charger, by the end of the second minute the first joystick is at 5%, second is at 1%;
  • at the beginning of the third minute connect second joystick to the charger, after this minute the first joystick is at 3%, the second one is at 2%;
  • continue the game without changing charger, by the end of the fourth minute first joystick is at 1%, second one is at 3%;
  • at the beginning of the fifth minute connect first joystick to the charger, after this minute the first joystick is at 2%, the second one is at 1%;
  • at the beginning of the sixth minute connect second joystick to the charger, after this minute the first joystick is at 0%, the second one is at 2%.

After that the first joystick is completely discharged and the game is stopped.

题目大意：两个人在打隔膜，有两个操纵杆，但只有一个充电器，充电器同时只能给一个操纵杆充电。每秒初可以选择一个操纵杆连上充电器，每过一秒没有充电的操纵杆减少2单位电，充电的操纵杆增加1单位电。如果某一秒初有操纵杆没电了或还有1单位电但没有选择给它充电，则游戏立即结束。求最多可以让游戏持续多少时间。

刚开始一直觉得是贪心之类的东西，但过不了，后来才反应过来是个傻逼DP。。。

B. Beautiful Paintings
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

There are n pictures delivered for the new exhibition. The i-th painting has beauty ai. We know that a visitor becomes happy every time he passes from a painting to a more beautiful one.

We are allowed to arranged pictures in any order. What is the maximum possible number of times the visitor may become happy while passing all pictures from first to last? In other words, we are allowed to rearrange elements of a in any order. What is the maximum possible number of indices i (1 ≤ i ≤ n - 1), such that ai + 1 > ai.

Input

The first line of the input contains integer n (1 ≤ n ≤ 1000) — the number of painting.

The second line contains the sequence a1, a2, ..., an (1 ≤ ai ≤ 1000), where ai means the beauty of the i-th painting.

Output

Print one integer — the maximum possible number of neighbouring pairs, such that ai + 1 > ai, after the optimal rearrangement.

Examples
input
5
20 30 10 50 40
output
4
input
4
200 100 100 200
output
2
Note

In the first sample, the optimal order is: 10, 20, 30, 40, 50.

In the second sample, the optimal order is: 100, 200, 100, 200.

题目大意：给出一个序列$a$，要重新排列这个序列，使得满足$a_i<a_{i+1}$的$i$最多。

将原序列排序，反复从中取出最长上升（注意不是不降）子序列接在结果序列后面，这样求出的答案一定是最优的。

C. Watchmen
time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Watchmen are in a danger and Doctor Manhattan together with his friend Daniel Dreiberg should warn them as soon as possible. There are n watchmen on a plane, the i-th watchman is located at point (xi, yi).

They need to arrange a plan, but there are some difficulties on their way. As you know, Doctor Manhattan considers the distance between watchmen i and j to be |xi - xj| + |yi - yj|. Daniel, as an ordinary person, calculates the distance using the formula .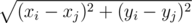

The success of the operation relies on the number of pairs (i, j) (1 ≤ i < j ≤ n), such that the distance between watchman i and watchmen j calculated by Doctor Manhattan is equal to the distance between them calculated by Daniel. You were asked to compute the number of such pairs.

Input

The first line of the input contains the single integer n (1 ≤ n ≤ 200 000) — the number of watchmen.

Each of the following n lines contains two integers xi and yi (|xi|, |yi| ≤ 109).

Some positions may coincide.

Output

Print the number of pairs of watchmen such that the distance between them calculated by Doctor Manhattan is equal to the distance calculated by Daniel.

Examples
input
3
1 1
7 5
1 5
output
2
input
6
0 0
0 1
0 2
-1 1
0 1
1 1
output
11
Note

In the first sample, the distance between watchman 1 and watchman 2 is equal to |1 - 7| + |1 - 5| = 10 for Doctor Manhattan and 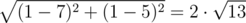 for Daniel. For pairs (1, 1), (1, 5) and (7, 5),(1, 5) Doctor Manhattan and Daniel will calculate the same distances.

题目大意：给出一些点，求欧几里得距离和曼哈顿距离相等的点对数。

显然答案是横坐标相等或纵坐标相等的点对数，分别求出两者并减去横纵坐标都相等的点对数。

D. Image Preview
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

Vasya's telephone contains n photos. Photo number 1 is currently opened on the phone. It is allowed to move left and right to the adjacent photo by swiping finger over the screen. If you swipe left from the first photo, you reach photo n. Similarly, by swiping right from the last photo you reach photo 1. It takes a seconds to swipe from photo to adjacent.

For each photo it is known which orientation is intended for it — horizontal or vertical. Phone is in the vertical orientation and can't be rotated. It takes b second to change orientation of the photo.

Vasya has T seconds to watch photos. He want to watch as many photos as possible. If Vasya opens the photo for the first time, he spends 1 second to notice all details in it. If photo is in the wrong orientation, he spendsb seconds on rotating it before watching it. If Vasya has already opened the photo, he just skips it (so he doesn't spend any time for watching it or for changing its orientation). It is not allowed to skip unseen photos.

Help Vasya find the maximum number of photos he is able to watch during T seconds.

Input

The first line of the input contains 4 integers n, a, b, T (1 ≤ n ≤ 5·105, 1 ≤ a, b ≤ 1000,1 ≤ T ≤ 109) — the number of photos, time to move from a photo to adjacent, time to change orientation of a photo and time Vasya can spend for watching photo.

Second line of the input contains a string of length n containing symbols 'w' and 'h'.

If the i-th position of a string contains 'w', then the photo i should be seen in the horizontal orientation.

If the i-th position of a string contains 'h', then the photo i should be seen in vertical orientation.

Output

Output the only integer, the maximum number of photos Vasya is able to watch during those T seconds.

Examples
input
4 2 3 10
wwhw
output
2
input
5 2 4 13
hhwhh
output
4
input
5 2 4 1000
hhwhh
output
5
input
3 1 100 10
whw
output
0
Note

In the first sample test you can rotate the first photo (3 seconds), watch the first photo (1 seconds), move left (2 second), rotate fourth photo (3 seconds), watch fourth photo (1 second). The whole process takes exactly 10 seconds.

Note that in the last sample test the time is not enough even to watch the first photo, also you can't skip it.

题目大意：手机上有$n$张照片，初始时显示的是第$1$张照片，可以花$a$秒切换到前一张或后一张照片，第$1$张的前一张是第$n$张，第$n$张的后一张是第$1$张。如果碰到没看过的照片就必须花$1$秒欣赏一下，如果照片是横的还要另外花$b$秒旋转照片，如果看过了就可以直接跳过。现在有$T$秒时间，求最多可以欣赏的照片数。

显然一定是先向左看一些照片，走回起点再向右看一些照片（或者反一下，先向右再向左），否则一定可以用更少的时间看相同数量的照片。这样看起来复杂度还是不对，但实际上枚举在一边看的照片数时，可以利用单调性直接维护折返后看的照片数。

E. Table Compression
time limit per test
4 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Little Petya is now fond of data compression algorithms. He has already studied gz, bz, zip algorithms and many others. Inspired by the new knowledge, Petya is now developing the new compression algorithm which he wants to name dis.

Petya decided to compress tables. He is given a table a consisting of n rows and m columns that is filled with positive integers. He wants to build the table a' consisting of positive integers such that the relative order of the elements in each row and each column remains the same. That is, if in some row i of the initial tableai, j < ai, k, then in the resulting table a'i, j < a'i, k, and if ai, j = ai, k then a'i, j = a'i, k. Similarly, if in some column j of the initial table ai, j < ap, j then in compressed table a'i, j < a'p, j and if ai, j = ap, j then a'i, j = a'p, j.

Because large values require more space to store them, the maximum value in a' should be as small as possible.

Petya is good in theory, however, he needs your help to implement the algorithm.

Input

The first line of the input contains two integers n and m (, the number of rows and the number of columns of the table respectively.

Each of the following n rows contain m integers ai, j (1 ≤ ai, j ≤ 109) that are the values in the table.

Output

Output the compressed table in form of n lines each containing m integers.

If there exist several answers such that the maximum number in the compressed table is minimum possible, you are allowed to output any of them.

Examples
input
2 2
1 2
3 4
output
1 2
2 3
input
4 3
20 10 30
50 40 30
50 60 70
90 80 70
output
2 1 3
5 4 3
5 6 7
9 8 7
Note

In the first sample test, despite the fact a1, 2 ≠ a21, they are not located in the same row or column so they may become equal after the compression.

题目大意：给出一个矩阵$A$，求一个正整数矩阵$B$，要求$B$的行和列上的相对大小与$A$相同，即满足

$\forall a_{i,j}<a_{i,k},b_{i,j}<b_{i,k}\\
\forall a_{i,k}<a_{j,k},b_{i,k}<b_{j,k}\\
\forall a_{i,j}=a_{i,k},b_{i,j}=b_{i,k}\\
\forall a_{i,k}=a_{j,k},b_{i,k}=b_{j,k}$

求$\max b_{i,j}$最小的矩阵$B$。

用结点代表矩阵的元素构造一张图。首先把相等的那些元素缩成一个点，这个用并查集维护即可。然后每个点分别向它所在的行和列的大于它的最小元素连边（没有就不连），边权为$1$。这样显然会形成DAG，在上面跑拓扑排序，各个点的答案就是距它最远的入度为$0$的点到它的距离。

代码在此。

Category: 题解 | Tags: DP 拓扑排序 贪心 数学 图论 并查集 Codeforces 容斥 | Read Count: 1170
Small_feed 评论 (1)
1
[回复]
Avatar_small
WasteRice 说:
Mar 11, 2016 09:22:05 PM

woc E题我Tarjan缩点真是萎傻了


登录 *


loading captcha image...
(输入验证码)
or Ctrl+Enter

Host by is-Programmer.com | Power by Chito 1.3.3 beta | Theme: Aeros 2.0 by TheBuckmaker.com